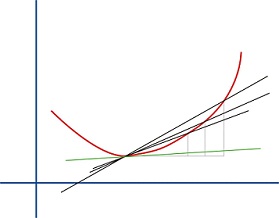
Se califica como derivada, a nivel gramatical, a cada palabra que surge por derivación. Los expertos en Química, por su parte, hacen alusión a este término para reconocer a una sustancia que se ha podido obtener a partir de otro producto, mientras que en Matemática la idea de derivada apunta a indicar la medida del punto límite entre el aumento del valor de una función y el crecimiento de la variable independiente.

Si uno profundiza en este tema y combina conocimientos para entender ciertas relaciones y cálculos, logra encontrar (y distinguir) múltiples clases de derivadas, cada una con rasgos exclusivos y propiedades únicas. Entre ellas aparece la logarítmica, un recurso que contribuye a hacer más fácil el cálculo de derivadas ordinarias que exigen la regla del producto.

Para Geometría Diferencial y cálculos vectoriales, en cambio, resultan más útiles las derivadas parciales detectadas en una función de muchas variables. Algo similar ocurre con las derivadas covariantes, que brindan la posibilidad de trabajar y hacer cálculos diferenciales con coordenadas curvilíneas. Y si hacemos referencia a las derivadas parciales, no debemos olvidar a las derivadas direccionales, que generalizan a las anteriores por ser direccionales en los vectores que resultan paralelos a los ejes.

En Álgebra y Topología Diferencial, asimismo, entra en juego la llamada derivada de Lie, la regla del producto de Leibniz y la derivación tensorial.

Cabe destacar que, más allá de estas posibilidades, existen las derivadas de una función inversa, las derivadas superiores, la derivada total, la derivada de Radon-Nikodym y la derivada fraccional, por señalar otras a modo de referencia.

Cuando alguien pide prestada una cierta suma de dinero a una persona física o a una entidad y no la devuelve en tiempo y forma, contrae una deuda. Hay, en la práctica, una gran cantidad de categorías vinculadas a esta palabra, incluso permitiendo que el término trascienda la cuestión monetaria.

En primer lugar, es posible distinguir a las deudas públicas (a nivel Estado) y a las deudas de carácter privado (que involucran a un individuo en particular por sus decisiones particulares).

Asimismo, existen las deudas amortizables (aquellas del Estado que se amortizan en los plazos que prevé la legislación), las deudas consolidadas (son deudas públicas con carácter perpetuo), la deuda exterior (de carácter público, se abona fuera del país con divisa extranjera), la deuda interior (deuda pública que se cubre, con moneda nacional, en la nación de origen), las deudas flotantes (aquellas que pueden incrementarse o disminuir a diario porque no están consolidadas y poseen vencimientos a término fijo) y las deudas tributarias (de acuerdo a los expertos en Derecho, son aquellas que surgen a partir de la liquidación tributaria).

Lejos de estas clasificaciones, aparecen expresiones que amplían el alcance práctico de la noción, tal como sucede con las deudas morales (aquellas que abarcan compromisos que deben saldarse por cuestiones de ética y moral), las deudas jurídicas (en las cuales la parte deudora está en falta frente a la acreedora) y la deuda antropológica (en una sociedad primitiva, el jefe o líder está en deuda con la comunidad por darle confianza, prestigio y poder). En un marco informal, además, alguien puede sentir que está en deuda con alguien o algo por no haberle dado todo de si mismo. Por ejemplo: “Siento que estoy en deuda con la gente, esperaban mucho de mí en la selección y creo que no logré satisfacer sus expectativas con mi desempeño”.

El individuo que busca trabajo y no consigue ser contratado por ninguna empresa o entidad, o bien ha sufrido un despido en el corto plazo y no encuentra otra posibilidad laboral pese a llevar su currículum a un gran número de compañías, enfrenta una situación de desempleo.

Según cómo surja, por cuánto tiempo se extienda y qué características presente este paro o cese forzoso de actividades laborales, el desempleo puede encuadrarse en múltiples categorías.

Existe, por ejemplo, el desempleo estructural, un fenómeno que puede afectar a muchas personas durante una buena cantidad de tiempo porque no se soluciona con un simple recurso de ajuste económico. Por lo general, está relacionado al desempleo cíclico (consecuencia del desgaste de un ciclo económico) y al desempleo de raíz tecnológica (ocasionado a partir de una revolución tecnológica).

El desempleo friccional, en cambio, es aquel que se enfrenta en el periodo de transición entre el último trabajo desarrollado y el encuentro de una nueva oportunidad laboral. Las estaciones del año, por su parte, influyen en la oferta y demanda de empleo provocando variaciones en el desempleo estacional.

Cabe resaltar además que, cuando la falta de trabajo se padece durante más de seis meses, suele hacerse alusión al desempleo de larga duración, mientras que se apela a la categoría de “desempleo abierto” para aludir a la realidad de quien carece de empleo, está en condiciones de iniciar una actividad de forma inmediata y busca trabajo de manera activa. Hay quienes, asimismo, frenaron la búsqueda de empleo por estar aguardando una respuesta por parte de un eventual empleador y entonces atraviesan un periodo de desempleo de iniciadores.

La palabra es fundamental para poder generar y sostener un diálogo. Esta exposición de ideas e intercambio de información u opinión suele desarrollarse en diferentes ámbitos bajo múltiples modalidades.

Cuando ninguna de las partes involucradas en la conversación repara en lo expresado por el otro y no se presta atención porque cada uno sostiene su verdad sin analizar lo dicho por el interlocutor, por señalar una posibilidad, se describe la situación a partir de la expresión “diálogo de sordos”. De no existir coherencia o un hilo conductor lógico, en tanto, adquiere relevancia la denominación de “diálogo de besugos”.

Otras alternativas incluyen a los diálogos a partir de lenguaje de señas, diálogos en alguna lengua extranjera y diálogos interreligiosos, por mencionar más a modo de referencia.

Es interesante tener en cuenta que, más allá de entablar u oir en nuestra vida cotidiana diálogos informales de raíz espontánea (se arman diálogos de temática y extensión variable entre vecinos; médicos y pacientes; compañeros de trabajo o de estudio; miembros de una misma familia; choferes y pasajeros; profesores y alumnos; comerciantes y clientes, etc), hay un amplio número de diálogos estructurados, de contenido formal (a veces, académicos y didácticos) que se planifican y organizan en función de presentaciones académicas, conferencias o discursos.

De vincularlo al mundo de las letras, por otra parte, encontraremos un género literario de corte clásico que admite clasificaciones de acuerdo a la época y los subgéneros donde ha sido cultivado. Así, entonces, se distinguen al diálogo platónico, al diálogo lucianesco, al diálogo ciceroniano, al diálogo renacentista, etc.

Para poder seleccionar el método más efectivo para alcanzar el fin deseado, en todos los casos es fundamental la información. Por esa razón, hoy describiremos diferentes propuestas de depilación a fin de orientar e informar a todas las personas que, por alguna razón, deseen o necesiten depilar alguna parte de su cuerpo.

Cabe recordar que la depilación surge a partir del acto de depilar, es decir, de remover y arrancar vello o pelo para mantener a la piel libre de ellos. A diferencia de lo que mucha gente puede llegar a creer, esta práctica no es exclusiva del universo femenino ni de una cierta edad: los hombres también apelan a esta acción para quitarse el vello no deseado.

Mientras que algunas personas apelan a métodos de depilación temporales, otras prefieren invertir más dinero y someterse a tratamientos de depilación definitiva, aunque hay quienes alertan sobre los riesgos de esta clase de procedimientos.

Si nos centramos en las alternativas de depilación casera, la solución más rápida es la de usar afeitadora o máquinas descartables de depilar, aunque exige una frecuencia mayor respecto a otras opciones porque no quita el vello desde la raíz. La depilación con cera (puede ser fría o caliente) es otra posibilidad para tener en cuenta en el hogar, al igual que la decoloración del vello (aunque no depila, disimula el pelo a través de productos químicos) y las cremas depilatorias.

Más complejas (y que requieren consultas y muchas precauciones a la hora de elegirlas para evitar problemas en la piel) son las técnicas de depilación definitiva por electrólisis y la depilación láser, por señalar dos de las más utilizadas.

Tener un peso adecuado y darle importancia a la alimentación sana y equilibrada es fundamental para gozar de buena salud. No cualquier persona puede (ni necesita) hacer dieta (ni para engordar ni para adelgazar), por eso hay que trabajar el cuerpo y la mente para desarrollar seguridad, aceptar el propio organismo y priorizar el bienestar general antes que la estética socialmente aceptada.

Claro que no siempre el concepto de dieta tiene una connotación negativa porque el término no se reduce a suprimir comidas o limitar la alimentación para bajar de peso. Se puede hacer alusión, por ejemplo, a la dieta mediterránea para indicar que hay pueblos cercanos a la cuenca del mar Mediterráneo donde abundan el vino, las legumbres, el aceite de oliva y los cereales a la hora de elaborar comidas.

La dieta carnívora (tal vez una de las más extendidas a nivel mundial), en cambio, se distingue por darle prioridad a las carnes, mientras que la dieta vegetariana evita precisamente la carne. Más extremista es la dieta vegana, donde se excluyen todos los productos que provengan de un animal por respeto a la vida en todas sus formas. Otra opción es la dieta omnívora, donde se combinan tanto alimentos de origen vegetal como animal.

Cabe destacar por otra parte que, según el cuadro de cada paciente, los nutricionistas pueden llegar a recomendar dietas hipocalóricas (cuando existe, por ejemplo, obesidad), dietas hiperproteicas (por anorexia, bajo peso, etc), dietas sin gluten (orientadas a las personas celíacas) y dietas bajas en grasas (para gente que presenta patologías del corazón), por señalar otras posibilidades. En ciertos momentos, frente a una intoxicación, los médicos también suelen indicar algunos días de dieta líquida para limpiar el organismo y evitar molestias gastrointestinales.

Quien lleva una vida sana y desea mantenerse en buen estado físico suele practicar, a lo largo de los años, uno o más deportes. Las disciplinas deportivas son numerosas y, además de ofrecer alternativas para todo tipo de preferencia, se adapta a las condiciones corporales y capacidades de cada individuo.

La mayoría de los deportistas suele desarrollar la actividad de manera amateur pero también hay quienes se dedican al deporte de manera profesional, en circuitos competitivos.

Asimismo, es posible hacer alusión a los deportes olímpicos (disciplinas que se incluyen en los Juegos Olímpicos tanto de invierno como de verano, tales los casos del atletismo, la natación, el baloncesto, el ciclismo, etc).

La gente más audaz, por su parte, se anima a poner a prueba su habilidad y resistencia física a través de deportes extremos, que desafían límites de tiempo, superficie y altura para añadirles dificultad y peligro. Los deportes de aventura (como buceo, windsurf y salto bungee) también aparecen como parte de los deportes extremos.

Si tenemos en cuenta el medio en el cual puede llegar a desarrollarse una actividad deportiva, en cambio, podemos distinguir entre deportes náuticos y deportes aéreos, entre otros.

Es importante tener presente por otra parte la existencia de deportes adaptados para que todas las personas que padecen una discapacidad tengan la posibilidad de divertirse, mostrar su talento y ejercitarse con alguna disciplina deportiva. Hay, por ejemplo, torneos de baloncesto adaptado (los jugadores compiten en sillas de ruedas), así como de natación adaptada (para deportistas con discapacidad visual, parálisis cerebral, etc), por indicar dos a modo de referencia.

Un despido es consecuencia del acto de despedir (o echar) algo o a alguien. Este término suele estar por lo general muy relacionado al ámbito laboral pero, asimismo, se utiliza en otros ámbitos y asociado a distintas clases de cuestiones.

En el marco de un empleo se pueden reconocer, a grandes rasgos, despidos procedentes (aquellos que se ajustan a los tiempos y formas planteados por la legislación vigente en cada país) y despidos improcedentes (cuando no están adecuados a la ley). Hay, además, despidos masivos (cuando una empresa deja sin trabajo a mucha gente a la vez), despidos nulos (si se indica como excusa una causa que la legislación invalida), despidos por cláusulas (régimen más común en la esfera pública que en el ámbito privado), despidos por fuerza mayor, despidos regulados (el sistema más común a escala internacional) y libres despidos (genera rechazo por no ofrecer garantías de seguridad laboral al trabajador). Las razones a la hora de fundamentar un despido son varias, algunas más creíbles y aceptadas que otras, como sucede al plantear la necesidad de achicar el personal para reducir gastos, el mal desempeño de las funciones del empleado despedido, etc.

Más allá de esta aplicación concreta del vocablo, es posible encontrar otras modalidades de uso. “Me despido de ti con un abrazo a la distancia y el deseo de verte pronto”, puede llegar a leerse en una carta o, en una consulta médica, un paciente le puede explicar al profesional: “Doctor, estoy preocupado porque desde hace varios días despido sangre por la boca”.

Entre la amplia variedad de herramientas que uno suele tener en su hogar para realizar refacciones menores o resolver cuestiones cotidianas aparece el destornillador.

Este elemento, fundamental para ajustar o aflojar tornillos, puede tener diferentes formas y tamaños, por eso es interesante conocer las variedades existentes y conseguir algunas de ellas para poder trabajar, en cada caso, con el destornillador más adecuado.

A grandes rasgos, se pueden diferenciar los destornilladores básicos de uso manual frente a los destornilladores eléctricos. La forma de las puntas también da lugar a múltiples categorías: hay destornilladores con puntas planas, otros que terminan en cruz, existen asimismo destornilladores de estrellas con cuatro o seis puntas y destornilladores con puntas hexagonales, por citar varios a modo de referencia.

Para trabajos específicos, en tanto, se recomienda el uso de destornilladores especiales de precisión, como ocurre en el campo de la relojería, donde se manipulan piezas diminutas. De querer comprobar si un conductor tiene conexión con una fase de la red de corriente alterna, en cambio, se usará un destornillador buscapolos.

El destornillador de impacto, el destornillador flexible, el destornillador multipuntas (que ofrece un único mango y distintas clases de cabezales), el destornillador quirúrgico y el destornillador triangular son otras variedades que se adaptan a otros requerimientos.

Muy diferente es el caso del destornillador sónico (tal como se conoce a una herramienta utilizada en la serie británica de ficción Doctor Who), así como del Destornillador entendido como un cóctel logrado a partir de la combinación de zumo de naranja con vodka.

El acto de difundir, es decir, expandir, propagar, divulgar o hacer circular algo (un aroma, un dato, un gas, etc) es parte del proceso de difusión.

El rol de los comunicadores, por ejemplo, guarda relación estrecha con la difusión de información. Hay en este marco difusión de contenidos periodísticos, difusión de escuchas telefónicas, difusión de datos de investigación, etc.

En el mundo de los negocios, en tanto, adquiere gran importancia la difusión de innovaciones, que se lleva adelante con herramientas de marketing y estrategias publicitarias.

En un contexto de aculturación, por otra parte, no se puede pasar por alto la difusión cultural, gracias a la cual se conocen y transmiten valores de una colectividad a otra.

Distinto es el caso de los expertos en Física, quienes señalan como difusión a un proceso de carácter irreversible en el cual se incrementa el desorden molecular a partir de la incorporación a un medio de partículas que se disuelven en él. Es posible distinguir, de acuerdo a las características de cada fenómeno, entre difusión intersticial, difusión sustitucional y difusión neta, además de reconocer a la difusión facilitada, la difusión en el sistema respiratorio y la difusión simple, entre otras.

Para hacer posibles los servicios de telefonía móvil, asimismo, se emplea una tecnología conocida como “difusión de celda”, así como para transmitir contenidos se usa una tecnología de tipo inalámbrico denominada difusión móvil integrada. Para minimizar el ruido de una imagen, en otro orden de cosas, hay expertos que aprovechan un procedimiento conocido como difusión anisotrópica.