Quienes se especializan en Geometría utilizan el concepto de paralelogramo para identificar al cuadrilátero en el cual los lados que se oponen resultan paralelos entre sí, es decir, no se unen nunca y son congruentes (esto significa que presentan la misma longitud).

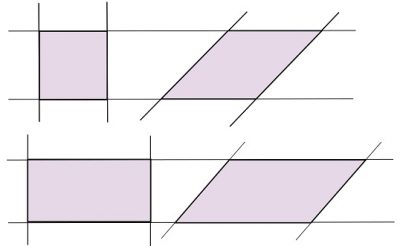De acuerdo a las particularidades que evidencien en relación a sus lados, es posible segmentarlos, según corresponda en cada caso, en el grupo de paralelogramos equiláteros (aquellos donde los dos pares de lados son iguales, como ocurre con el rombo y el cuadrado) o en el de los paralelogramos no equiláteros (en los cuales hay diferencias entre los lados). Es interesante destacar que, más allá de los contrastes que puede haber entre las figuras, todas las clases de paralelogramos son convexas.

Los formatos que presente cada uno de ellos, por otra parte, determinarán si cada cuadrilátero pertenece al conjunto de los paralelogramos rectángulos (como el rectángulo propiamente dicho y el cuadrado) o al de los paralelogramos no rectángulos u oblicuángulos (como ocurre con el romboide y el rombo).

Al profundizar en este tema se advierte también que existe una clase especial de paralelogramo bautizado con el mismo nombre del teorema que lo descubre: se trata del teorema (y del paralelogramo) de Varignon, identificación inspirada en el francés Pierre Varignon. Este postulado señalar que, en todo cuadrilátero, los puntos medios de los lados permiten armar un paralelogramo cuya área cubre la mitad de la figura original. En este marco, puede determinarse que el denominado paralelogramo de Varignon es un cuadrado siempre que las diagonales del cuadrilátero posean igual longitud y sean perpendiculares.

Parénquima es un concepto que, según se advierte al informarse sobre sus significados y aplicaciones, se utiliza tanto en el campo de la Anatomía como en el área de la Botánica para hacer alusión a una clase de tejido. En el primer caso, es el propio de los órganos glandulares, mientras que en el segundo se trata de un tejido vegetal conformado por células de apariencia cúbica o esférica que se distribuyen de modo separado llenando espacios libres dejados por diferentes tejidos y órganos.

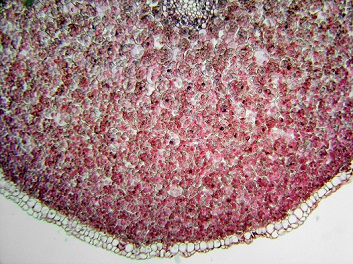Al profundizar en el grupo de parénquima vegetal descubrimos, a la vez, numerosas subcategorías que demuestran el amplio alcance de la noción.

Existe, por señalar una posibilidad concreta que sume datos de interés sobre el tema, el parénquima de relleno compuesto por células de un mismo diámetro que cubren espacios, así como también se identifica al parénquima vascular que se encarga de proteger a los tejidos conductores de las plantas.

El parénquima acuífero, en tanto, es propio de la vegetación xerófila, mientras que el parénquima aerífero es típico de la vegetación de hidrófitos. El parénquima amilífero, conocido asimismo como de reserva, es quien se encarga de almacenar ciertos nutrientes para beneficio de la planta. Por su parte, el parénquima clorofílico (o parénquima asimilador, tal su otra denominación aceptada) es el que lleva a cabo el proceso de fotosíntesis, ya sea en la versión de parénquima esponjoso (propio de la parte carnosa de las frutas, las hojas y los tallos) o en la de parénquima en empalizada (el cual posee numerosas vacuolas y cloroplastos).

Las obsesiones se describen como perturbaciones anímicas motivadas por una idea o pensamiento puntual que de manera recurrente está en la mente de quien no logra librarse del tema que acapara toda su atención y lo lleva a desarrollar diversas clases de acciones en función de esa cuestión.

Los cuadros no son siempre iguales. Hay quienes, por ejemplo, tienen obsesiones amorosas que manifiestan idealizando a alguien e intentando poseer de cualquier manera a esa persona por considerar que solamente pueden ser felices si tienen su atención y afecto, así como también hay casos de obsesiones vinculadas a la alimentación que desencadenan desequilibrios nutricionales a raíz de hábitos alimenticios que no son saludables pero que responden al deseo descontrolado de calmar la ansiedad o el estrés comiendo o evitando la comida, según cada cuadro. Las obsesiones religiosas, las obsesiones laborales y las obsesiones relacionadas a cuestiones sexuales son otras posibilidades que demuestran la diversidad de este panorama.

Las obsesiones relacionadas a la limpieza y el orden, en tanto, llevan a quien las padece a ordenar donde y cuando no es necesario, a revisar una y otra vez que todo esté perfectamente ubicado en el lugar asignado, a limpiar aunque nada esté sucio y a sentir miedo y ansiedad por considerar que todo está contaminado.

A nivel más general, es posible diferenciar a las obsesiones autógenas (surgen de modo súbito y sin motivaciones aparentes) frente a las obsesiones reactivas (aquellos que se desencadenan por factores externos fáciles de identificar que el individuo cree importantes como para querer revertirlos y solucionarlos).

Cuando uno consulta el diccionario de la Real Academia Española (RAE) para conocer el significado preciso de obsidiana descubre que esta palabra de origen latino identifica a una roca volcánica de carácter vítreo que tiene una tonalidad oscura. Se trata, de acuerdo a quienes analizaron su origen, sus particularidades y sus aplicaciones, de un feldespato que se funde de manera natural y que, en otros tiempos, fue aprovechado por indios americanos para elaborar espejos, flechas y armas cortantes.

Hay quienes definen a este material como “piedra de la justicia” porque le reconocen el poder de potenciar la verdad y la recomiendan para favorecer los momentos de meditación. Según se cuenta, los mayas y los aztecas usaban a la obsidiana para el arte de la adivinación.

A lo largo del tiempo se fueron reconociendo múltiples tipos de obsidiana, por eso es interesante conocer las alternativas al respecto ya que, en función de las particularidades de cada una, se las puede emplear como piedras preciosas, trabajos ornamentales, elemento quirúrgico, arma o para fabricar la base de un tocadisco, por ejemplo.

La obsidiana negra, capaz de absorber energía, es la más común, pero también existe la obsidiana arcoíris a la cual se le reconoce la capacidad de brindar protección y ser ideal para cuestiones esotéricas y rutinas de meditación.

La obsidiana manto huichol en la que mucha gente confía para poder superar diversas circunstancias de la vida, la obsidiana dorada que contribuye a la iluminación y a la comprensión a nivel espiritual, la obsidiana caoba que potencia la determinación y el coraje, la obsidiana telaraña que favorece la tranquilidad mental y la obsidiana plateada asociada a la humildad y a la pureza en el camino hacia la verdad son otras variedades disponibles.

La elocuencia al expresarse de manera oral y el saber asumir el rol de orador se describen, de acuerdo a la teoría, como oratoria. Esta palabra, además, identifica a un género literario donde aparecen los sermones, las conferencias, los discursos y las disertaciones, entre otras modalidades.

El número de personas que, en un evento o circunstancia especial, toman la palabra permite establecer si se trata de una oratoria grupal (con al menos dos individuos hablando) o de una oratoria individual (el uso de la palabra es exclusivo de un único sujeto).

Las temáticas abordadas y el tipo de receptor del mensaje, en tanto, le dan importancia a clasificaciones como las de oratoria académica (asociada a cuestiones científicas o literarias que puedan servir para informar, enseñar y transmitir saberes), oratoria demostrativa o epidíctica (focalizada en sucesos pasados y orientada a un público que no posee influencia sobre el tema desarrollado ni capacidad para juzgarlo), oratoria deliberativa o política (dirigida a hechos futuros, planteando cuestiones útiles y provechosas y marcando aquello que el orador considera perjudicial para que los participantes puedan interiorizarse sobre ellos, opinar y votar) y la de oratoria judicial o forense (sobre actos pasados, acerca de los cuales el orador plantea acciones que, a su criterio, son justas o injustas). Es interesante tener en cuenta además que los predicadores suelen hacer uso de la denominada oratoria sagrada para realizar sus sermones u oficios religiosos, la cual se asocia al género político o deliberativo, conjunto donde aparece además como opción a tener en cuenta la oratoria militar.

Con mínimos conocimientos de geografía, historia, economía y política uno consigue herramientas para poder saber que en el mundo hay numerosas clases de países, cada uno con particularidades que marcan diferencias respecto al resto de las naciones.

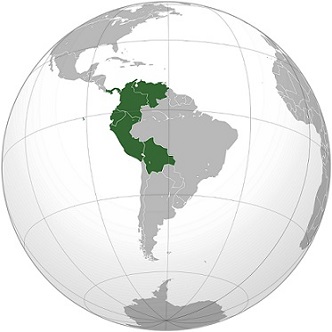Es posible distinguir, por detallar un caso a modo de ejemplo, a los países desarrollados (donde los habitantes, en general, gozan de una excelente calidad de vida y hay herramientas para la innovación y la tecnología al servicio de la población) frente a aquellos que están en vías de desarrollo (con economías que parten de un estado de transición y están en pleno desarrollo económico) y a los países subdesarrollados (en los cuales son nulas o muy escasas la capacidad productiva, el progreso y la riqueza).

Tampoco las superficies son las mismas para cada territorio: hay países más grandes que otros, así como también hay países con salida al mar y otros sin litoral.

La religión, en tanto, es una variable que invita a distinguir entre países musulmanes, países católicos, países hindúes, países judíos, etc, mientras que el tipo de gobierno predominante marca la existencia de países democráticos y países autocráticos.

El lenguaje, por agregar otra posibilidad, permite aludir según corresponda a países de habla francesa, países de habla inglesa, países de habla portuguesa, países de habla neerlandesa y países de habla hispana, entre otras alternativas. De analizar el continente al cual pertenezca una nación, entonces ganarán relevancia las categorías de países americanos, países africanos, países europeos, países oceánicos y países asiáticos para poder definirlos en base a su ubicación.

El concepto de palta tiene varias aplicaciones prácticas. Por un lado, hace referencia a un pueblo amerindio que pobló el norte de Perú y una región de Ecuador donde en la actualidad se ubica la provincia de Loja, así como a la lengua jíbara propia de esta comunidad; por otro, alude a un fruto comestible que también se conoce como aguacate. Palta Meléndez, en tanto, es el nombre artístico de un imitador y actor chileno llamado Juan Carlos Meléndez Mackenzie.

De hacer foco en el alimento y sus variedades, descubriremos que, si bien la clase que más se cultiva y consume a escala mundial es la llamada palta Hass, hay otras alternativas a tener en cuenta, como el caso de la recientemente descubierta palta GEM, la cual posee una maduración tardía y cautiva a fuerza de un intenso sabor y una textura cremosa.

La palta fuerte procedente de Centroamérica y el suelo mexicano cuya carne es fácil de separar de la piel áspera, la palta Bacon de piel verde y fina, y la palta Negra de la Cruz propia de Chile de aspecto oscuro o morado son otras opciones que le aportan diversidad al producto. Según de qué modo se las cultive, además, se podrán obtener paltas orgánicas.

Independientemente del tipo de palta elegido, es posible clasificar a este fruto de acuerdo a cómo se las prepare. Las paltas fritas, las paltas gratinadas, las paltas rellenas y la palta como ingrediente de una ensalada son propuestas que seducen a un gran número de consumidores.

A la hora de condimentar diversas comidas, es frecuente que se tenga en cuenta al orégano, una planta cuyas hojas se destacan por su aroma y su sabor. Asimismo, es un producto con propiedades medicinales que se puede disfrutar en infusión o preparar con él un aceite esencial y hasta una crema para beneficiar la salud.

Existe en el mundo una amplia variedad de orégano y numerosas especies que comúnmente se bautizan con esta misma palabra, razón por la cual es interesante informarse sobre el tema para aprender a diferenciar a cada planta en función de sus características.

Una de las alternativas es el llamado orégano de cerro, tal como se define a una planta medicinal natural del territorio mexicano que pertenece a la familia de las asteráceas. El orégano brujo o francés, en tanto, integra la familia de las lamiáceas y es aprovechado como antimicótico, desinfectante y estimulante muscular, aunque hay investigaciones que alertan sobre sus efectos y grados de toxicidad. Orégano grueso, por otra parte, es el nombre común de una planta del grupo de las verbenáceas que se localiza en Colombia, Venezuela, Cuba, México y Puerto Rico, entre otros países. El orégano acuático, que crece a escala mundial en sitios húmedos, gana relevancia como producto medicinal por tener poder antiséptico, cicatrizante, purgante y digestivo.

Para evitar arruinar platos por no prepararlos con los ingredientes adecuados, es fundamental identificar qué y cómo es el orégano común, la hierba aromática que le aporta un sabor único a salsas, quesos y pizzas, por ejemplo. Es posible conseguir orégano fresco o bien utilizar orégano seco.

El concepto de organismo se utiliza con frecuencia para aludir a un determinado ser vivo, pero también se aprovecha para hacer referencia a instituciones, dependencias y oficinas pertenecientes a una cierta entidad.

Según el contexto en el cual se emplee esta palabra, podremos diferenciar muchas clases de organismos, segmentándolos por categorías de acuerdo a su origen, a sus rasgos particulares y a su vigencia, entre otras variables.

Si una única célula compone a un ser viviente, por ejemplo, ganará protagonismo la expresión “organismo unicelular”, así como aquellos que poseen al menos un par de células se describen como organismos multicelulares o pluricelulares.

Hay, por otra parte, organismos presentados como autótrofos que tienen la capacidad de valerse de sustancias inorgánicas para desarrollar su propia materia orgánica y organismos señalados como heterótrofos que se alimentan a partir de otros seres vivos porque no logran transforman las sustancias inorgánicas en materia orgánica. Los organismos hermafroditas, los organismos aerobios y anaerobios, los organismos fotosintéticos, los organismos transgénicos, los organismos microscópicos, los organismos vertebrados, los organismos procariotas, los organismos eucariotas, los organismos terrestres, los organismos acuáticos, los organismos aéreos, los organismos ovíparos y los organismos en peligro de extinción conforman otros conjuntos que demuestran la gran variedad de especímenes que pueblan este planeta y el interesante abanico de opciones que extienden el alcance de la palabra ‘organismo’.

Al interpretar este vocablo como institución, en cambio, tendremos la posibilidad de distinguir entre organismos internacionales, nacionales y regionales, organismos centralizados y descentralizados y entre organismos gubernamentales y no gubernamentales, por agregar algunas referencias al respecto.

Dada la gran cantidad de aplicaciones que posee el concepto de orbital, resulta importante tener siempre presente su significado y estar al tanto de todas sus interpretaciones.

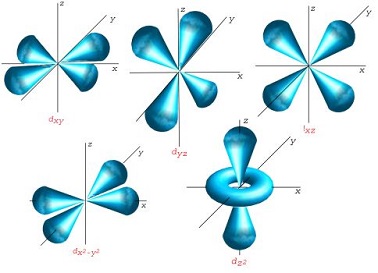De acuerdo a la teoría, esta palabra se utiliza en el campo de la Física para aludir a cómo la densidad de la carga de un electrón se distribuye en torno al núcleo de una molécula o átomo. A nivel más general, en tanto, funciona como adjetivo para describir a todo aquello que guarde relación con una órbita.

En Anatomía, por señalar un caso puntual, este vocablo se usa para reconocer a los huesos que componen la órbita de cada ojo, mientras que en la llamada Mecánica Celeste adquiere relevancia la expresión “resonancia orbital” para narrar la influencia gravitatoria de carácter regular existente entre las órbitas de un par de cuerpos.

Al buscar diversas clases de orbitales tenemos la posibilidad de centrar la atención en los orbitales atómicos (entre los cuales aparecen el orbital s, el orbital p, el orbital d y el orbital f) o en los orbitales moleculares (surgidos por la fusión de orbitales atómicos tras el enlace de dos átomos). Dentro de este último grupo señalado hay orbitales σ enlazantes, orbitales π enlazantes, orbitales σ* antienlazantes, orbitales π* antienlazantes y orbitales n). Los orbitales no enlazantes o no enlaces, por su parte, poseen una densidad electrónica parecida a la que tienen los átomos que intervienen en él.

Tampoco se puede dejar de hacer referencia a los orbitales atómicos híbridos, los cuales están vinculados a la geometría molecular y tienen la particularidad de superponerse en la formación de enlaces.