En Tipos.com.mx, como pueden advertir al repasar el archivo de este sitio, ya hicimos una referencia general a las sucesiones y detallamos las clases que pueden reconocerse al poner el foco en las sucesiones de carácter matemático.
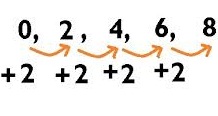 Hoy, como todavía queda información para aportar al respecto, retomaremos la temática y mencionaremos diversos tipos de sucesiones numéricas.
Hoy, como todavía queda información para aportar al respecto, retomaremos la temática y mencionaremos diversos tipos de sucesiones numéricas.
Dentro de este conjunto adquiere relevancia, por ejemplo, la sucesión de Fibonacci, tal como se conoce a la sucesión infinita de cifras pertenecientes al grupo de los números naturales.
Asimismo, es posible distinguir sucesiones numéricas finitas (aquellas donde se puede establecer cuál es el último término), sucesiones numéricas de perfil constante (cuando todos los términos tienen un único valor) y sucesiones numéricas monótonas, las cuales pueden ordenarse de forma creciente o decreciente. Es decir: sin importar a qué familia corresponda cada número (enteros, naturales, etc) existe la opción de armar una sucesión ascendente (1,2,3,4,5,6,7,8,9,10) o bien descendente (-5,-4,-3,-2,-1).
De profundizar en esta temática y averiguar los rasgos distintivos de otras sucesiones de números, entonces conoceremos cómo son y de qué modo se arman las sucesiones alternadas, además de interiorizarnos acerca de las sucesiones numéricas convergentes y las sucesiones numéricas acotadas, por agregar otras a las descriptas líneas arriba.
Asimismo, en función de las necesidades de quien arme o analice una estructura de este tipo, se puede trabajar con sucesiones de números pares o impares; sucesiones numéricas de múltiples de una determinada cifra; sucesiones de cuadrados de números naturales; sucesiones numéricas de una cierta potencia, etc.

 Entre las opciones que se tienen en cuenta para embellecer ventanales o puertas de vidrio (como las que suelen dar acceso a un balcón) aparece el voile, una tela liviana y semitransparente de la cual hay infinidad de colores y diseños. Otros, en cambio, prefieren trabajar con organdí para lograr el típico efecto almidonado que caracteriza a esta muselina.
Entre las opciones que se tienen en cuenta para embellecer ventanales o puertas de vidrio (como las que suelen dar acceso a un balcón) aparece el voile, una tela liviana y semitransparente de la cual hay infinidad de colores y diseños. Otros, en cambio, prefieren trabajar con organdí para lograr el típico efecto almidonado que caracteriza a esta muselina. Antes del repaso de alternativas, resulta apropiado mencionar que, después de tantos años de investigaciones y avances en el plano tecnológico, ya hay teorías científicas que han quedado obsoletas; otras, en cambio, se mantienen vigentes. Asimismo, hay teorías científicas modernas y teorías científicas que, según se llegó a comprobar tiempo después, resultaron ser falsas.
Antes del repaso de alternativas, resulta apropiado mencionar que, después de tantos años de investigaciones y avances en el plano tecnológico, ya hay teorías científicas que han quedado obsoletas; otras, en cambio, se mantienen vigentes. Asimismo, hay teorías científicas modernas y teorías científicas que, según se llegó a comprobar tiempo después, resultaron ser falsas. En primer lugar, resulta interesante destacar que las dimensiones corporales y las habilidades son criterios que se tienen en cuenta al segmentar a la familia de los terrier. Se pueden reconocer, por ejemplo, varios terriers de trabajo. Algunos de ellos tienen extraordinarias capacidades para rastrear y acorralar presas, mientras que otros se reservan para matar a ciertas especies. Dentro de este grupo, asimismo, se distinguen los terrier de caza y los fell terrier.
En primer lugar, resulta interesante destacar que las dimensiones corporales y las habilidades son criterios que se tienen en cuenta al segmentar a la familia de los terrier. Se pueden reconocer, por ejemplo, varios terriers de trabajo. Algunos de ellos tienen extraordinarias capacidades para rastrear y acorralar presas, mientras que otros se reservan para matar a ciertas especies. Dentro de este grupo, asimismo, se distinguen los terrier de caza y los fell terrier.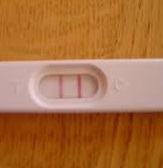 Hay, como se advierte con un mínimo de información sobre el tema, muchos métodos para confirmar si se está en la dulce espera, pero por lo general el primero que se realiza es un test casero con un dispositivo que se compra en las farmacias o comercios similares. Esta pieza (una tira química que reacciona minutos después de recibir unas pocas gotas de orina) es fácil de conseguir, tiene un precio razonable y es sencilla de utilizar. Si el sistema detecta la presencia de una hormona conocida como gonadotropina coriónica humana, el resultado será positivo. Claro que se requieren estudios más precisos para confirmar el diagnóstico ya que a veces surgen falsos positivos en las pruebas de embarazo de venta libre.
Hay, como se advierte con un mínimo de información sobre el tema, muchos métodos para confirmar si se está en la dulce espera, pero por lo general el primero que se realiza es un test casero con un dispositivo que se compra en las farmacias o comercios similares. Esta pieza (una tira química que reacciona minutos después de recibir unas pocas gotas de orina) es fácil de conseguir, tiene un precio razonable y es sencilla de utilizar. Si el sistema detecta la presencia de una hormona conocida como gonadotropina coriónica humana, el resultado será positivo. Claro que se requieren estudios más precisos para confirmar el diagnóstico ya que a veces surgen falsos positivos en las pruebas de embarazo de venta libre. Se trata de un invento tecnológico reservado a usos específicos, generalmente vinculados al plano de las investigaciones científicas. De querer saber más sobre estos dispositivos por simple curiosidad o por motivaciones académicas, tal vez les resulten de gran interés los
Se trata de un invento tecnológico reservado a usos específicos, generalmente vinculados al plano de las investigaciones científicas. De querer saber más sobre estos dispositivos por simple curiosidad o por motivaciones académicas, tal vez les resulten de gran interés los  A lo largo de los años, muchas clases de termostatos alcanzaron relevancia a nivel mundial. Varios de ellos, según resaltan quienes los utilizan en un ámbito laboral o los comercializan, aún siguen vigentes pese a los avances registrados al respecto con ayuda de la
A lo largo de los años, muchas clases de termostatos alcanzaron relevancia a nivel mundial. Varios de ellos, según resaltan quienes los utilizan en un ámbito laboral o los comercializan, aún siguen vigentes pese a los avances registrados al respecto con ayuda de la  De tener origen en un gobierno cuyas autoridades pretenden generar miedo en los ciudadanos para llevar a cabo propósitos sin riesgo a ser enfrentados, se hace alusión al terrorismo de Estado, aunque existen muchas otras categorías en las cuales se ramifica este concepto. A fin de ayudarlos a saber qué modalidades de terrorismo se han detectado en distintos momentos de la Historia en diferentes lugares del mundo, a continuación ofreceremos más detalles sobre el uso práctico de esta noción que hoy hemos querido abordar en
De tener origen en un gobierno cuyas autoridades pretenden generar miedo en los ciudadanos para llevar a cabo propósitos sin riesgo a ser enfrentados, se hace alusión al terrorismo de Estado, aunque existen muchas otras categorías en las cuales se ramifica este concepto. A fin de ayudarlos a saber qué modalidades de terrorismo se han detectado en distintos momentos de la Historia en diferentes lugares del mundo, a continuación ofreceremos más detalles sobre el uso práctico de esta noción que hoy hemos querido abordar en  De analizar la oferta comercial en materia de taquetes, hallaremos opciones fabricadas en plástico, otras de metal y hasta alternativas químicas (estas últimas, ideales para superficies huecas). Asimismo, encontraremos propuestas como los taquetes de expansión (proporcionan una seguridad mayor al fijar de manera permanente un tornillo en yeso, ladrillos, cemento o cualquier otro
De analizar la oferta comercial en materia de taquetes, hallaremos opciones fabricadas en plástico, otras de metal y hasta alternativas químicas (estas últimas, ideales para superficies huecas). Asimismo, encontraremos propuestas como los taquetes de expansión (proporcionan una seguridad mayor al fijar de manera permanente un tornillo en yeso, ladrillos, cemento o cualquier otro 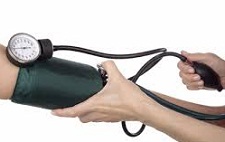 Lo interesante de hacer foco en el significado de esta palabra es que no sólo se relaciona al ámbito médico. Según se deduce de sus otras aplicaciones prácticas, existen tensiómetros que les sirven a los científicos para establecer la tensión superficial que presenta una sustancia en estado líquido y para calcular qué nivel de
Lo interesante de hacer foco en el significado de esta palabra es que no sólo se relaciona al ámbito médico. Según se deduce de sus otras aplicaciones prácticas, existen tensiómetros que les sirven a los científicos para establecer la tensión superficial que presenta una sustancia en estado líquido y para calcular qué nivel de